第9回アルゴリズム: 整列

第9回アルゴリズム: 整列#

この授業で学ぶこと#

今回の授業では、データの整列を題材にいくつかのアルゴリズムを紹介する。

アルゴリズムの主な目的は、問題を正確かつ効率的に解くことである。実はこれまでのテキストでも、練習問題や課題を通じて、アルゴリズムと言えるような手順をプログラムに起こす経験を積んできている。特に、どのような入力に対しても正しい答えを出力するようなプログラムを多く書いたと思うが、これがまさに問題を正確に解くということである。一方で、問題を効率的に解くことについては、これまであまり考えてこなかった。ここでは、整列のアルゴリズムの間に実行速度で差があることを見ていく。

なお、今回の演習課題は2種類の整列アルゴリズムを完成させて実行することとする。

ソートとは#

データをとある規則にもとづいて順番に並び替えることをソート（整列）という。例えば、整数のリスト

[8, 4, 5, 1, 2]

について、これを小さい順（昇順）にソートすると

[1, 2, 4, 5, 8]

となる。また大きい順（降順）にソートすると

[8, 5, 4, 2, 1]

となる。

文字列を辞書順にソートする操作もよく行われる。例えば、文字列のリスト

["carrot", "onion", "eggplant", "beet", "cabbage"]

を辞書順にソートすると

["beet", "cabbage", "carrot", "eggplant", "onion"]

となる。

今回は簡単のためリストデータのみを考え、さらに数値については昇順、文字列については辞書順に並べることに限定して考える。

ソートは使用頻度の高い基本的な操作なので、数多くのアルゴリズムが考案されている。今回はその中から代表的な挿入ソートとクイックソートを紹介する。

なお、実用上はリストの sort() メソッドや、組み込み関数の sorted() を使うことで簡単にソートすることができる。ここではアルゴリズムの学習のため、これらのメソッド・関数には頼らずに1からプログラムを作成することを考える。

リストの要素の交換

ソートアルゴリズムの実装では、リストの要素の交換をよく行う。例えば、x = [2, 3] というリストがあったとして、これの1番目と2番目の要素を入れ替えたいとする。

次のコードは意図した結果にならない。

x[0] = x[1]  # この時点で x = [3, 3] になる
x[1] = x[0]  # x = [3, 3]

上記の方法では上手くいかないので、変数の値を一時的に保存する tmp 変数を用意して次のように書くのが一般的な方法である。

tmp = x[0]
x[0] = x[1]
x[1] = tmp

Pythonでは、次のように簡潔な記法でも値を交換することができる。特に理由がなければ、以下の方法を使おう。

x[0], x[1] = x[1], x[0]

挿入ソート#

挿入ソートは、簡単に言えば左から順に整列する方法である。挿入ソートが数字を昇順に並び替える様子を、次の図に示す。

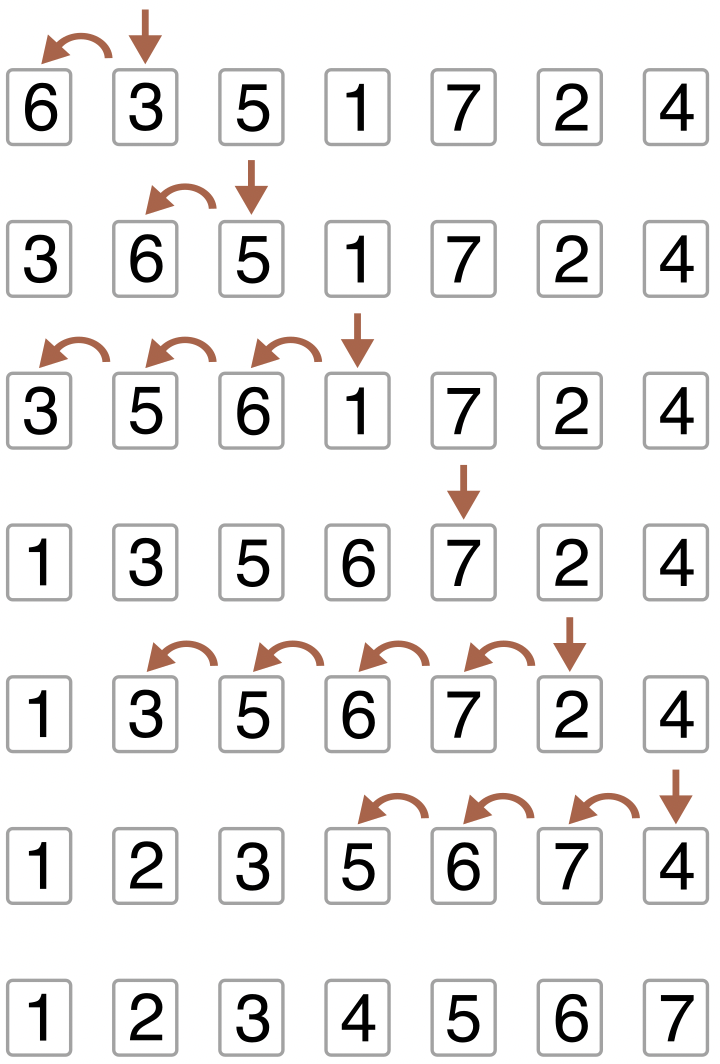
_images/insert_sort.png — Fig. 19 挿入ソート：ループごとの整列の様子#

あとで挿入ソートを insert_sort() 関数として実装するが、その内部でfor文を使用している。上図では、上から順にループ1回あたりの操作を示している。

要素数が7のとき全部で6回のループ処理が行われるが、各ループで行っていることを言葉にすると次の通りである。

1回目のループでは、左から2番目までの要素を昇順に並んだ状態にする。
2回目のループでは、左から3番目までの要素を昇順に並んだ状態にする。
…
6回目のループでは、左から7番目までの要素を昇順に並んだ状態にする。

トランプなどのカードゲームにおいて、カードを並び替えるときに挿入ソートに近い方法を取る人は多いのではないだろうか。それくらい直感的でわかりやすい方法である。

それでは、挿入ソートを実装してみよう。以下に未完成の insert_sort() 関数を用意した。 #ここに何か書く とある位置に1行のコードを追加することで、プログラムを完成させてみてほしい。

なお verbose というデフォルト引数により、オプションとして途中経過を出力できるようにしている。デフォルト値は False なので、単に insert_sort(x) と呼び出せば何も出力されない。一方で、insert_sort(x, True) や insert_sort(x, verbose=True) と呼び出すと途中経過を確認することができる。また関数に戻り値はなく、引数に渡した x を直接書き換えるコードとなっていることに注意する。

def insert_sort(x, verbose=False):  # verboseは詳細の意味
    for i in range(1, len(x)):
        key = x[i]  # 矢印の要素
        j = i - 1
        while j >= 0 and x[j] > key:
            # ここに何か書く
            j -= 1
            
        if verbose:
            print(f"{i}回目のループ終了時： {x}")
    return

x = [6, 3, 5, 1, 7, 2, 4]
insert_sort(x, verbose=True)
print(x)

クイックソート#

クイックソートは、リストを部分に分割し、それぞれに対して再帰的に整列を行うことで全体を整列する方法である。クイックソートが数字を昇順に並べる様子を、次の図に示す。

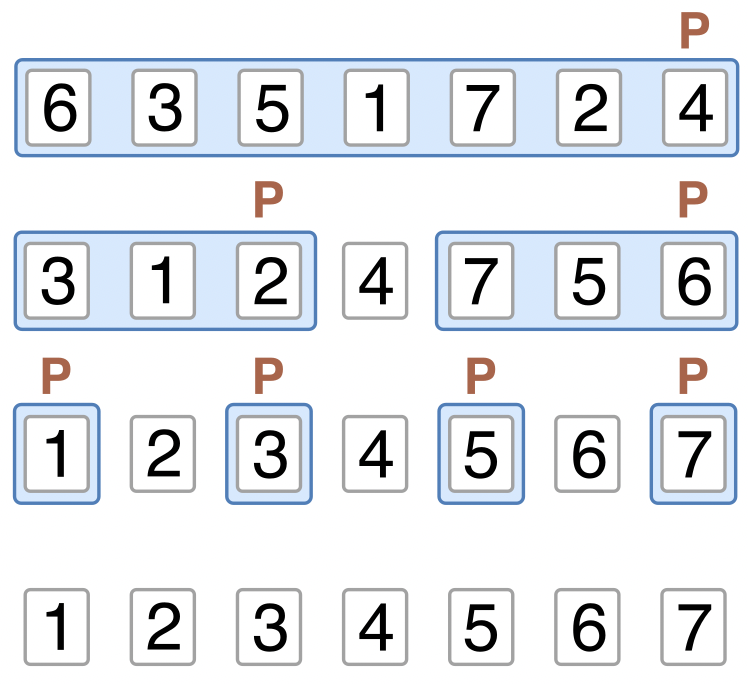
_images/quick_sort1.png — Fig. 20 クイックソート：再帰呼び出しごとの整列の様子#

あとでクイックソートを quick_sort() 関数として実装するが、その内部で再帰呼び出しを行っている。上図では、上から順に再帰呼び出しごとの操作を表しており、青の領域ごとに quick_sort() 関数を適用していることを表している。

それぞれの段で行っていることを言葉にすると次の通りである。

1段目ではリスト全体に対して quick_sort() を適用する。右端の要素をピボットとし、ピボットより小さい要素を左に寄せ、ピボット以上の要素を右に寄せ、それらの間にピボットを置く。
2段目では（1段目の）ピボットの両側について、それぞれに quick_sort() を適用する。それぞれのリストの右端の要素をピボットとし、それぞれのリスト内で先ほどと同様の処理を行う。
3段目では（2段目の）各ピボットの両側について、それぞれに quick_sort() を適用する。今回はどれも要素数1なので、並び替えは行われない。

1段目の操作の詳細を図示したものが、次の図である。

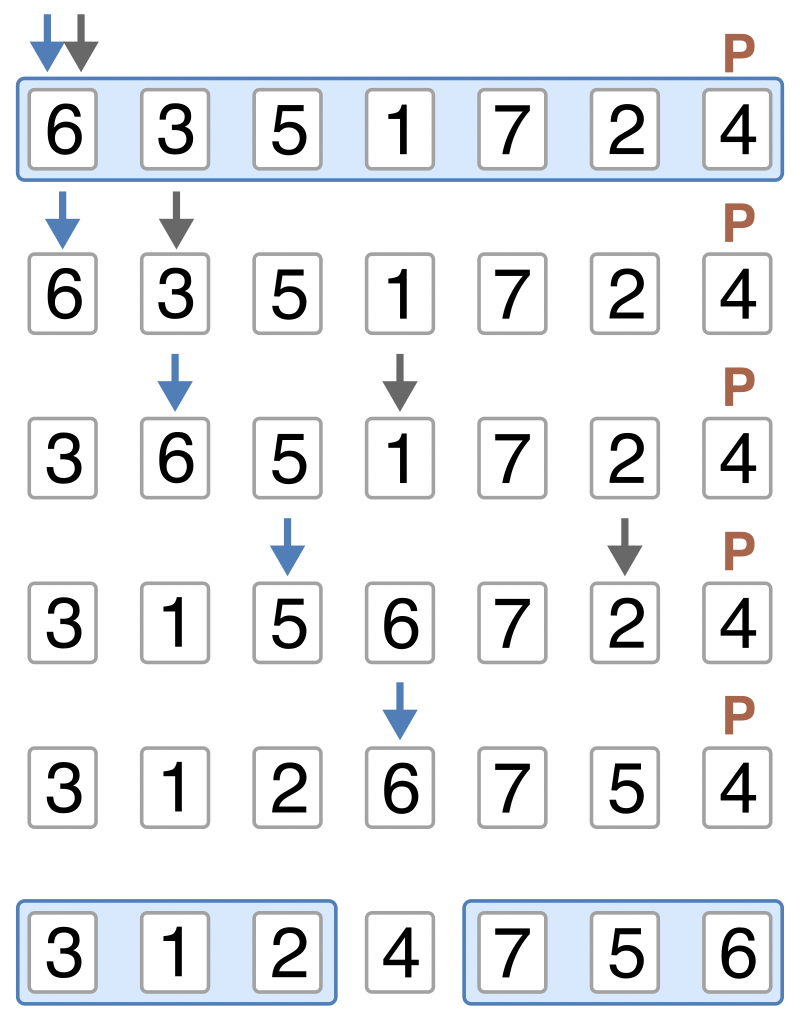
_images/quick_sort2.png — Fig. 21 クイックソート： `quick_sort1` 1段目の操作の詳細#

左端から順にピボットより小さい要素を埋めていく。左に位置する青矢印は次に埋めるべき位置を表している。青矢印と灰矢印を次のように動かしていく。

青矢印と灰矢印を1番目の要素からスタートさせる
灰矢印を1つずつ右へ進めていってピボットより小さい要素を探す
ピボットより小さい要素が見つかったら、両矢印の要素を交換し、青矢印を右へ1つ進めて2に戻る

（青矢印と灰矢印が同じ位置の場合は、交換しても何も起こらない）

ピボットより小さい要素が見つからなかったら、そこで処理を終了し、最後に青矢印の要素とピボットを交換する。

上記手順を終えると、[ピボットより小さい要素] [ピボット] [ピボット以上の要素] の順に要素が並んだ状態になる。あとはピボットの両側の要素に対して再帰的に quick_sort() 関数を適用すれば、全体が整列した状態にすることができる。

挿入ソートに比べるとあまり直感的な方法ではないと感じるかもしれないが、実はプログラミングの世界では典型的と言えるような問題の解き方をしている。このように問題を部分に分割して再帰的に解き、それらを合わせて全体の問題を解く方法を分割統治法（divide-and-conquer）という。

それでは、クイックソートを実装してみよう。以下に未完成の quick_sort() 関数を用意した。 #ここに何か書く とある位置に1行のコードを、return の手前に2行のコードを追加することで、プログラムを完成させてみてほしい。

なお insert_sort() 関数とは異なり、quick_sort() 関数はソートする範囲を left と right という引数で指定できるようにしている。 left は左端のインデックス、right は右端のインデックスを表す。これらの引数は、リストの一部分を再帰的にソートする際に必要になる。

def quick_sort(x, left, right, verbose=False):
    if right - left <= 0:
        return
    if verbose:
        print(f"quick_sort(x, {left}, {right}) 呼び出し時: {x}")
    
    pivot = x[right] # 右端をpivotとする
    
    i = left # i: 青矢印
    for j in range(left, right): # j: 灰矢印
        if x[j] < pivot:
            # ここに何か書く
            i += 1
            
    # pivotの値をi番目と交換することで、 xの中身は[pivot未満のデータ], pivot, [pivot以上のデータ] という順になる
    x[i], x[right] = x[right], x[i]
    
    if verbose:
        print(f"再帰呼び出し前： {x}\n")
        
    # ここに再帰呼び出しのコードを書く
    return

x = [6, 3, 5, 1, 7, 2, 4]
quick_sort(x, 0, len(x)-1, verbose=True)
print(x)

実行時間の比較#

挿入ソートとクイックソートの大きな違いとして、データ数が増えたときの実行時間の増え方が挙げられる。実験して確かめてみよう。

まず実行時間の測定方法について説明する。
exec_time() 関数は、algo で指定したソートの実行時間を測定し戻り値として返す。 timeモジュールの time.time() 関数を利用しているが、これはUNIX時間（1970年1月1日午前0時0分0秒からの経過秒数）を返す関数である。 exec_time() では、ソートの実行前後のUNIX時間の差から、ソートの実行時間を求めている。

import time

def exec_time(x, algo):
    start = time.time()
    if algo == "insert":
        insert_sort(x)
    else:
        quick_sort(x, 0, len(x)-1)
    end = time.time()
    return end - start

以下の generate_data() 関数は、ランダムな0以上1未満の小数を要素とするサイズ N のリストを生成する。生成されたリストを使って、ソートにかかる時間を測定してみよう。 N = 10**2 くらいまでは挿入ソートとクイックソートの間に大きな差はないが、N = 10**4 くらいになるとクイックソートの方が明らかに速いことが確かめられる。

import random

def generate_data(N):
    data = []
    for i in range(N):
        data.append(random.random())  # random.random()は0以上1未満の小数を返す
    return data

N = 10 ** 2
x1 = generate_data(N)
x2 = x1.copy()  # 同じデータを使用するためにコピーする

print(f"挿入ソートの実行時間: {exec_time(x1, 'insert'):.6f}")
print(f"クイックソートの実行時間: {exec_time(x2, 'quick'):.6f}")

第9回 アルゴリズム: 整列

Contents

第9回 アルゴリズム: 整列#