第10回 アルゴリズム: 探索#
この授業で学ぶこと#
今回の授業では、探索アルゴリズムについて学ぶ。またファイルの読み書きの方法についても学ぶ。
探索とは#
複数のデータの中から、特定の条件に適合するデータを見つけることを探索という。 このテキストでは、次の問題設定に限定して考える: 数値のリストと数値のキーが与えられるとき、リストの中にキーと一致する要素が存在するかを判定し、存在するときはそのインデックスを1つ求める。
このアルゴリズムを関数として実装しよう。
リストとキーを引数として受け取り、リストの中にキーが存在すればそのインデックスを返し、存在しなければ None を返す関数を作成する。
例えば、次のリストとキーのペアに対しては、インデックスの3を返す。
data = [5, 1, 3, 7, 2] key = 7
次のリストとキーのペアに対しては、None を返す。
data = [5, 1, 3, 7, 2] key = 4
探索は使用頻度の高い基本的な操作なので、数多くのアルゴリズムが考案されている。 今回はその中から代表的な線形探索と二分探索を紹介する。
なお、探索プログラムはリストの index() メソッドを使えば、次のように実装することができる。
ここではアルゴリズムの学習のため、index() メソッドには頼らずに1からプログラムを作成することを考える。
def search(data, key):
if key in data:
return data.index(key)
else:
return None
data = [5, 1, 3, 7, 2]
key = 7
print(search(data, key))
data = [5, 1, 3, 7, 2]
key = 4
print(search(data, key))
線形探索#
線形探索は、前から順に探すという単純なアルゴリズムである。
実装としては、for文により前から要素を1つずつ調べていき、キーに一致する要素を見つけたところでそのインデックスをreturn文で返す。
最後までキーに一致する要素が見つからなかった場合は、None をreturn文で返す。
以下に、未完成の linear_search() 関数を用意した。練習として、プログラムを完成させてみてほしい。
def linear_search(data, key):
for i in range(len(data)):
pass # ここを書き換える
return None
data = [5, 1, 3, 7, 2]
key = 7
print(linear_search(data, key)) # 3
data = [5, 1, 3, 7, 2]
key = 4
print(linear_search(data, key)) # None
解答例
def linear_search(data, key):
for i in range(len(data)):
if data[i] == key:
return i
return None
二分探索#
二分探索は、リストがソートされているという前提のもとで、より効率的な探索を実現するアルゴリズムである。
リストがソートされているとき、要素とキーの大小関係を調べることにより、キーがあるとしたら要素より右か左かが判明する。 二分探索ではこの性質を利用し、さらに大小関係を調べる要素を探索範囲の中央から選ぶことで、なるべく少ないステップで探索範囲を絞り込んでいく。
例としてキーが7のとき、二分探索が探索範囲を絞り込んでいく様子を次の図に示す。
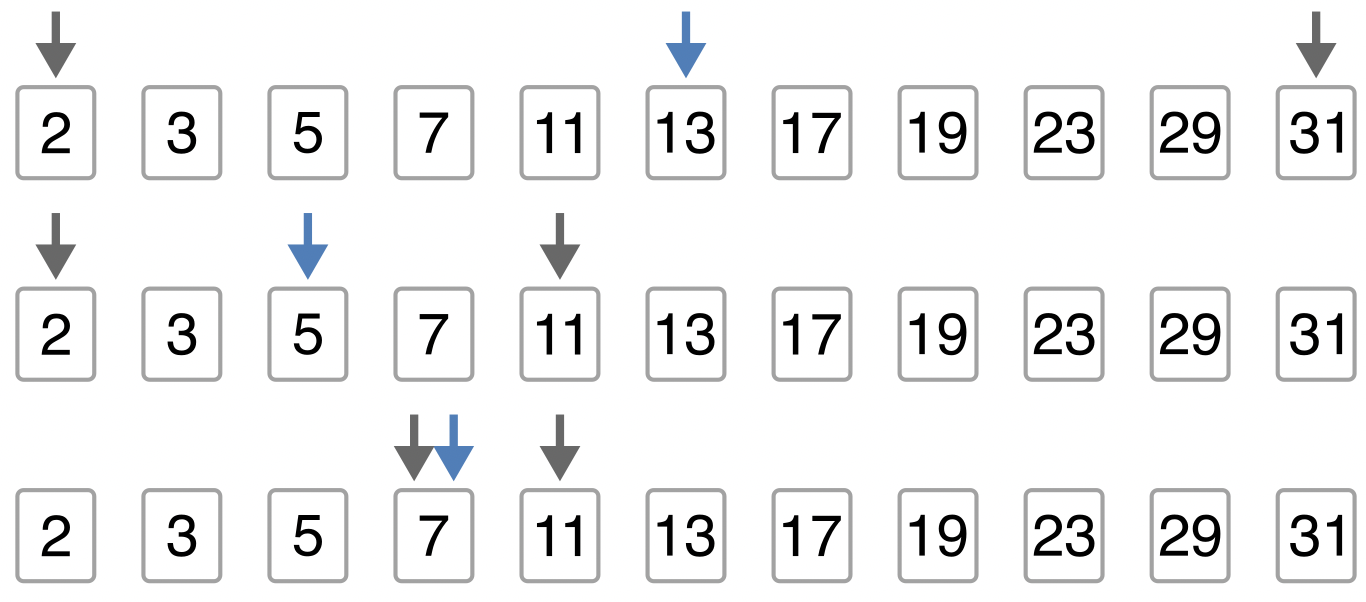
Fig. 22 キーが7のときの二分探索の様子#
両端の灰矢印が、探索範囲を表している。これらの中央の青矢印が、大小関係を調べる要素である。 1行目の比較では、青矢印の13よりキーの7の方が小さいので、キーがあるとしたらこれより左側にあると判断できる。 したがって、右の灰矢印を青矢印の1つ左に移動させて、次の行に移る。
2行目も同様にして、青矢印の5とキーの7を比較する。今度はキーの方が大きいので、左の灰矢印を青矢印の1つ右に移動させる。3行目までくると、探索範囲は2つ(7と11)に絞り込めている。このように探索範囲のサイズが偶数のときは、ちょうど中央の位置に要素はないので、中央の左隣か右隣の要素を比較対象に選ぶ(ここでは左隣を選択している)。このとき青矢印の要素はキーと一致するので、青矢印のインデックスを返して探索を終了する。
キーに一致する要素がない場合は、上記操作をくり返すと、いずれ灰矢印の位置が逆転する。このとき None を返して探索を終了する。
以下に、未完成の binary_search() 関数を用意した。
左の灰矢印に相当するのが left、右の灰矢印に相当するのが right、真ん中の青矢印に相当するのが mid である。
上の説明を参考に、プログラムを完成させてみてほしい。
def binary_search(data, key):
left = 0
right = len(data) - 1
while left <= right:
mid = (left + right) // 2
if data[mid] == key:
pass # ここを書き換える
elif data[mid] > key:
pass # ここを書き換える
else:
pass # ここを書き換える
return None
data = [1, 3, 5, 7, 9]
key = 7
print(binary_search(data, key)) # 3
data = [1, 3, 5, 7, 9]
key = 4
print(binary_search(data, key)) # None
解答例
def binary_search(data, key):
left = 0
right = len(data) - 1
while left <= right:
mid = (left + right) // 2
if data[mid] == key:
return mid
elif data[mid] > key:
right = mid - 1
else:
left = mid + 1
return None
ここまでに紹介した3つの探索方法について、実際に計算時間を比較してみよう。
ここでは自明な例ではあるが、\(0\) から \(N-1\) まで整数が順に並んだリスト data を list(range(N)) により作成し、それに対して探索を実行している。
import time
def exec_time(func, data, key):
start = time.time()
func(data, key)
end = time.time()
return end - start
N = 10**7
data = list(range(N))
key = N // 3 # 適当な要素
print(exec_time(search, data, key))
print(exec_time(linear_search, data, key))
print(exec_time(binary_search, data, key))
ファイルの入出力#
探索アルゴリズムから話題を変えて、この節ではファイルの入出力について学ぶ。 これまではPythonプログラムの中で閉じた話がほとんどであったが、ファイルの入出力を学ぶことで、パソコン上のファイルに対して自由な処理を行えるようになったり、プログラムの実行結果を永続的に保存できるようになったりするなど出来ることの幅がぐんと広がる。
Googleドライブのマウント#
Google Colab上でファイルを扱うために、最初にGoogleドライブに接続する必要がある(マウントという)。 ここではマウントの手順を説明する。
サイドメニューから以下の順番でアイコンをクリックする。
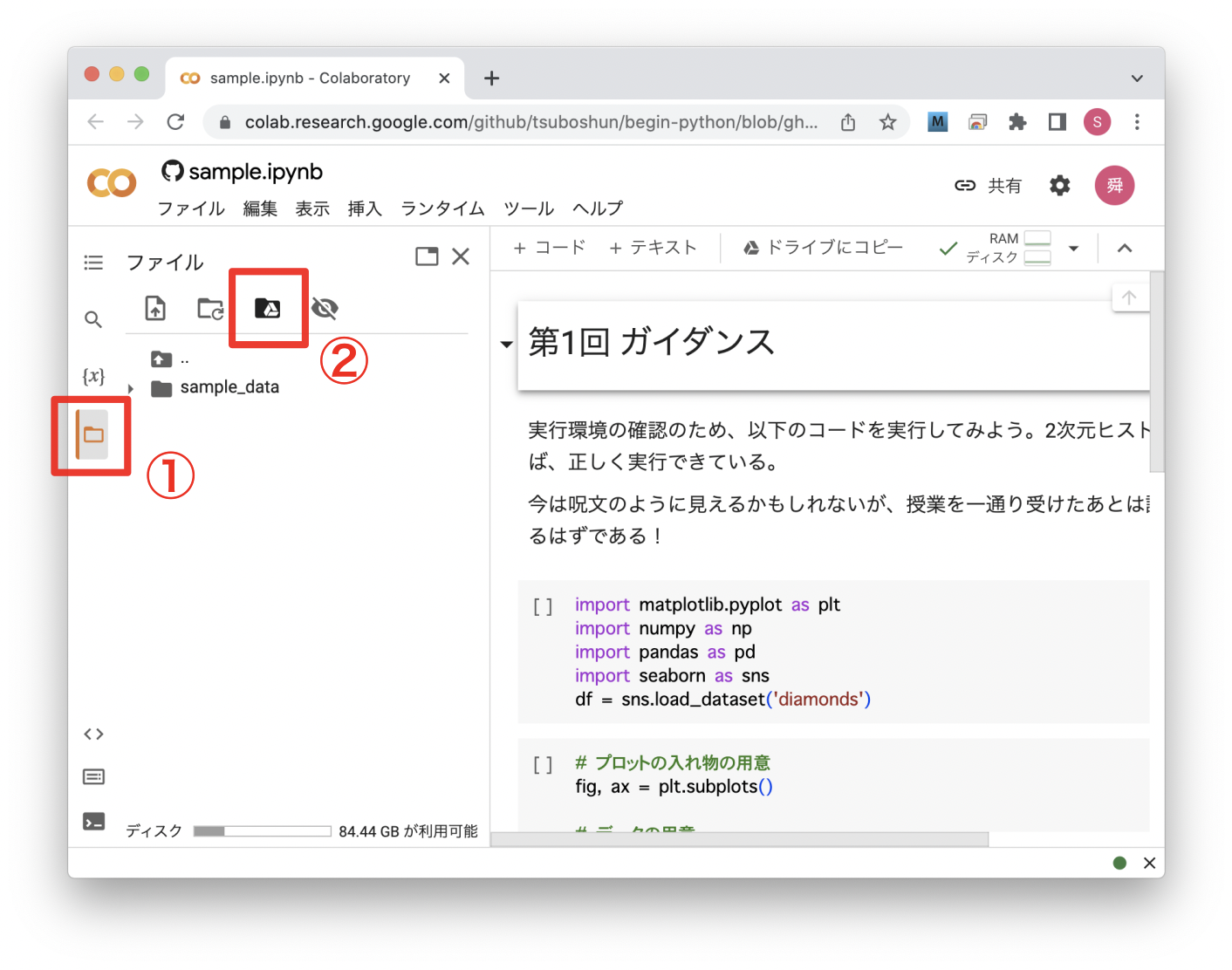
Fig. 23 Googleドライブのマウント#
そうすると以下のようなコードがノートブック上に現れるので、これを実行する。 実行するとアカウントのログイン画面が表示され、その後Googleドライブのマウントを許可するか聞かれるので、許可するを選択する。
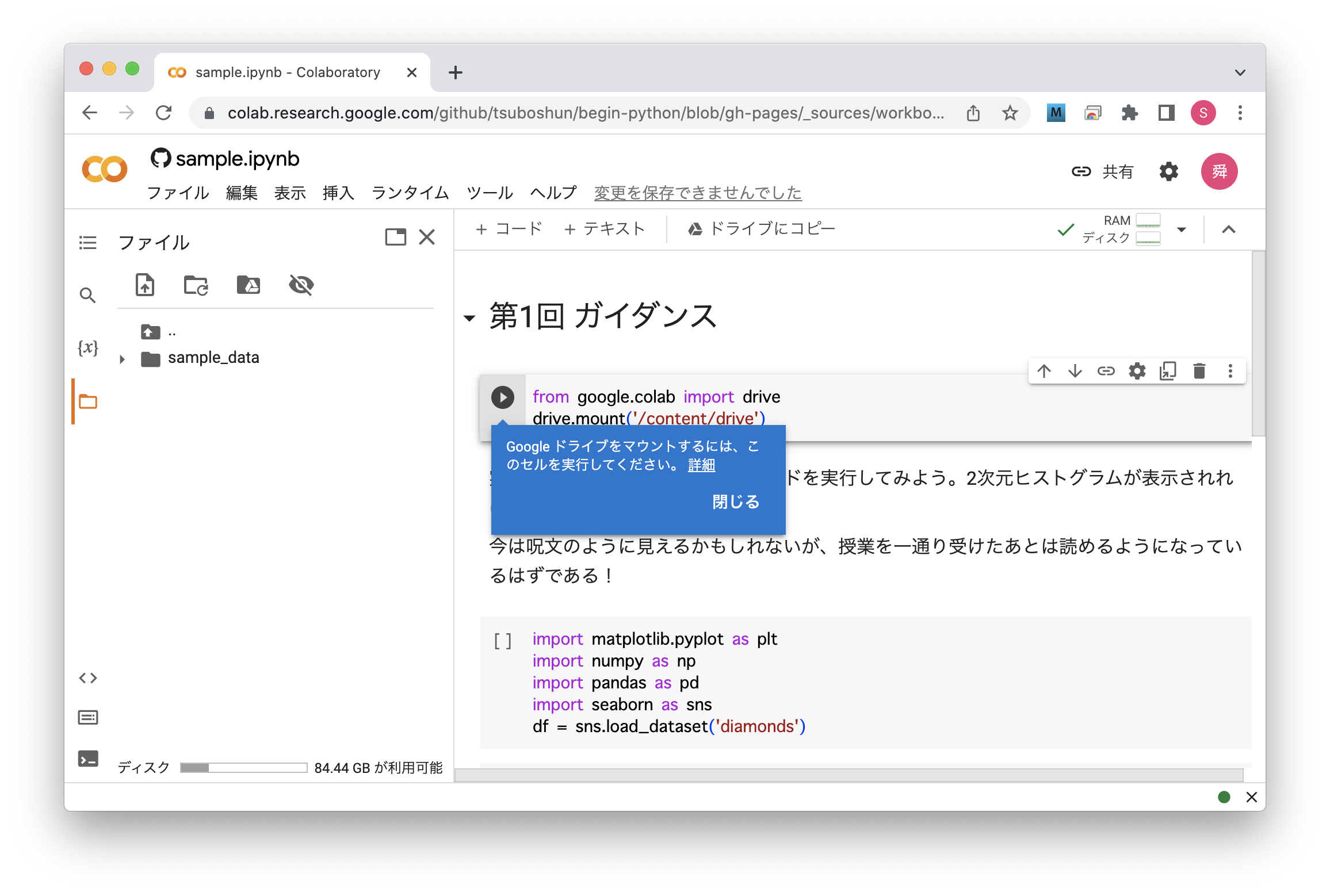
Fig. 24 Googleドライブのマウント#
マウントしたあと左のウィンドウ上で /content/drive/MyDrive を見に行くと、Googleドライブ上のファイル・フォルダが確認できるはずである。
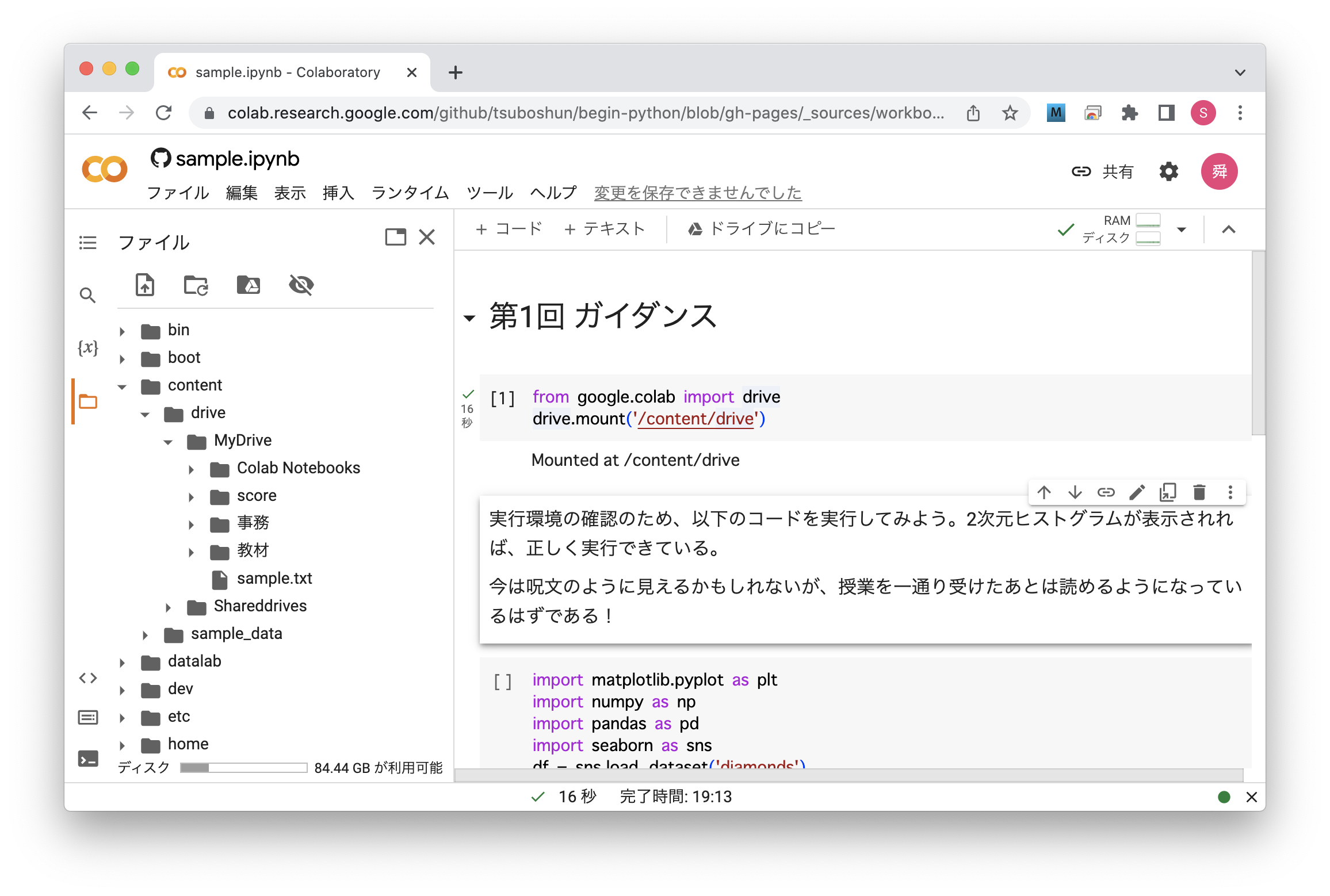
Fig. 25 Googleドライブのマウント#
ファイルの読み込み#
練習用のファイルとして次のデータが書かれたsample.txtを用意し(ToyoNet-ACEでも配布する予定)、Googleドライブのマイドライブ直下に置く。それ以外の場所に置いた場合は以降のコードの path を適宜変更する。
8 7 9 6 9 4 5 8 7 6 9 9 9 8 9 6 7 9 7 8
このファイルの中身は組み込み関数の open() を使って、次のように読み込むことができる。
path = "/content/drive/MyDrive/sample.txt"
f = open(path, mode='r')
content = f.read()
print(content)
f.close()
open() 関数は、第一引数にファイルの存在する場所(パスという)、第二引数にモードを渡す。
パスは文字列で表し、フォルダを1つ下るごとに / で区切って content フォルダからの位置関係を表現する。
第二引数に渡している 'r' は読み込みモードを表す。
open() 関数の返すファイルオブジェクト f に対して、read() メソッドを呼び出すと、ファイルの中身を文字列として取得できる。
最後に、開いたファイルオブジェクトを f.close() により閉じている。
read() メソッドはファイル全体を文字列として読み込むが、for文により一行ずつ読み込むこともできる。
f = open(path, mode='r')
for line in f:
print(line)
f.close()
さて sample.txt の中身は各行が一人一人の学生、各列が何かしらのスコアを表していたとしよう(つまり学生4人・スコア5つ)。このときデータを2次元リストとして読み込めると、分析の際に便利である。次のコードにより、ファイルの中身を2次元リストとして読み込むことができる。
f = open(path, mode='r')
data = []
for line in f:
data.append(line.strip().split(' '))
print(data)
f.close()
ここで各行の文字列 line について、まず strip() メソッドにより改行文字 \n を取り除き、次に split(' ') メソッドにより空白文字で区切ってリストに変換している。例として、line にファイルの1行目 "8 7 9 6 9\n" が代入されたときの処理の流れを、以下に示す。
line.strip().split(' ')
↓ line の指す値に置き換え
"8 7 9 6 9\n".strip().split(' ')
↓ strip() メソッドの適用
"8 7 9 6 9".split(' ')
↓ split() メソッドの適用
['8', '7', '9', '6', '9']
よって、data.append(line.strip().split(' ')) は data.append(['8', '7', '9', '6', '9']) と同じことであり、これにより2次元リスト data の末尾に1次元リスト ['8', '7', '9', '6', '9'] が追加される。
注意点として、この時点では data の各要素は文字列型となっている。そこで分析前に整数型または浮動小数点数型に変換しておく。
for i in range(len(data)):
for j in range(len(data[i])):
data[i][j] = int(data[i][j]) # 小数を含むならfloat()
data
ファイルの書き込み#
読み込んだデータをもとに各生徒の平均スコアを求めて、ファイルに出力してみよう。
まず出力用のパスを入力とは別に設定する。
open() 関数を書き込みモード('w') で呼び出し、書き込み用のファイルオブジェクト f を取得する。
平均値の計算は、ここでは簡単に総和を求める sum() 関数と len() 関数を使用して行っている。
そして結果を f.write() によりファイルに書き込んでいる。
入力と同じように1行1学生となるように、最後に改行 \n を入れている。
ファイルへの書き込みを終えたら、f.flush()、f.close() を順に呼び出してファイルを閉じる。
実は f.write() を呼び出した時点では、ファイルへの書き込みを予約した状態に過ぎず、OSの状態によっては実際の書き込みは後回しにされてしまう。
f.flush() は、ファイルへの書き込みを確実に完了させる働きを持つ。
output_path = "/content/drive/MyDrive/sample_mean.txt"
f = open(output_path, mode='w')
for lst in data:
mean = sum(lst) / len(lst)
f.write(f"{mean}\n")
f.flush()
f.close()
ここで紹介した書き込み方法では、毎回ファイルの内容が上書きされる。
そうではなく、ファイルの末尾に追記したい場合には追記モード('a') を指定する。
ファイルオブジェクトの使い方は書き込みモード('w')の場合と全く同じである。
演習#
課題
上の節では、各学生の平均スコアを求めてファイルに出力した。これを参考に、平均スコアの代わりにスコアの標準偏差を求めてファイルに出力し、作成したファイルをレポートに添付しなさい。ファイル名は sample_std.txt とすること。これは必須ではないが、可能なら小数は第3位を四捨五入して第2位までを求めなさい(参考)。
ヒント1: 第6回で紹介したNumPyを利用すると、標準偏差は簡単に求められる。import numpy as np によりNumPyを読み込んだあと、np.std() 関数を使って、np.std(lst) によりリスト lst の標準偏差を求めることができる。
ヒント2: 学生は4人いるので、標準偏差も4つ求まることになる。sample_std.txt は次のような見た目になる。ヒントとして1行目のみ答えを示す。つまり、data の1行目 [8, 7, 9, 6, 9] の標準偏差を求めて小数第3位を四捨五入すると 1.17 になる(四捨五入せずに1.16619…という解答でも正解とする)。
1.17 * * *
import numpy as np # NumPyの読み込み
output_path = "/content/drive/MyDrive/sample_std.txt"
f = open(output_path, mode='w')
for lst in data:
pass # ここに適切なコードを書く
f.flush()
f.close()